My first chess bot

2021-09-16

In my spare time, I’ve been slowly learning about reinforcement learning. I came upon this post by Andrew Healey about making a chess engine, and thought “I know all about AI, I’ll make a bot that beats his!”. Read on to see how that went.

Step one: Andoma vs. random bot

Andrew’s chess engine is called Andoma. See the code here: Andoma.

To get a better understanding of how to use Andoma, I made a random bot that it could play against. This way, I could quickly see how Andoma performs against a rubbish opponent. As expected, Andoma wins every game.

def andoma_vs_random():
    board = chess.Board()

    def move():
        return random_move(board) if board.turn == chess.WHITE else andoma_move(board)

    while not board.is_game_over():
        board.push(move())

    print('Random [W] vs Andoma [b]:')
    print(board)
    print(f"\nResult: [W] {board.result()} [b]")

def andoma_move(board: chess.Board) -> chess.Move:
    return next_move(1, board, debug=False)

def random_move(board: chess.Board) -> chess.Move:
    legal_moves = list(board.legal_moves)
    return random.choice(legal_moves)

The result:

Random [W] vs Andoma [b]:
r . . . . r k .
p p p . . p p p
. . p . . . . .
. . b . . . . .
. . . . . . . .
. . . n p . . .
. . . q . . . P
. . . K . . . R

Result: [W] 0-1 [b]

See notation to understand the output.

Step two: make a random bot with OpenSpiel

I’ve been playing with OpenSpiel, which comes with a bunch of algorithms and environments. It’s got an algorithm I want to use to fight Andoma, but my first baby step is to just make a simple bot. OpenSpiel comes with a chess implementation and a generic random bot. All games/environments share a common interface, so it’s simply a matter of hooking up the pieces:

game = pyspiel.load_game("chess")
player_1 = uniform_random.UniformRandomBot(0, np.random.RandomState())
player_2 = uniform_random.UniformRandomBot(1, np.random.RandomState())
players = [player_1, player_2]

state = game.new_initial_state()

while not state.is_terminal():
  current_player_idx = state.current_player()
  current_player = players[current_player_idx]
  action = current_player.step(state)
  state.apply_action(action)

If you’re interested in using OpenSpiel, my OpenSpiel playground can get you up and running with relative ease. OpenSpiel’s documentation is enough to cobble bits together, but you may end up needing to read some of the source code for specifics.

Step 3: MCTS

Time for a stronger opponent. Now that I’ve got OpenSpiel set up, I want to try its Monte Carlo Tree Search (MCTS) algorithm.

I’ve recently learned about MCTS. It’s more of a planning algorithm than a learning algorithm, but can be coupled with learning algorithms to make it more effective. This is the approach used by the various Alpha* agents, one of which famously beat world champion Lee Sedol in a Go match.

MCTS is somewhat similar to alpha-beta pruning (which Andoma uses), in that it explores a number of game trajectories from the current game state, and picks the most promising move based on the outcomes of those trajectories. The difference is that while Andoma only explores a few moves in advance, MCTS plays multiple games to completion from the current state (this is actually not the case for AlphaGo, but that’s beyond the scope of this post). The average outcome of games played from that state determines how ‘promising’ a state it is. For example, if you see 10 wins and 10 losses from one game state, but 18 wins and 2 losses from another state, then the latter state is more promising.

An advantage of this approach is that MCTS does not need any evaluation of intermediate game states or moves like Andoma does. MCTS only cares about the outcomes of completed games. In fact, a simple MCTS implementation can make random moves to simulate games from the current state. This is the default approach for the MCTS algorithm in OpenSpiel.

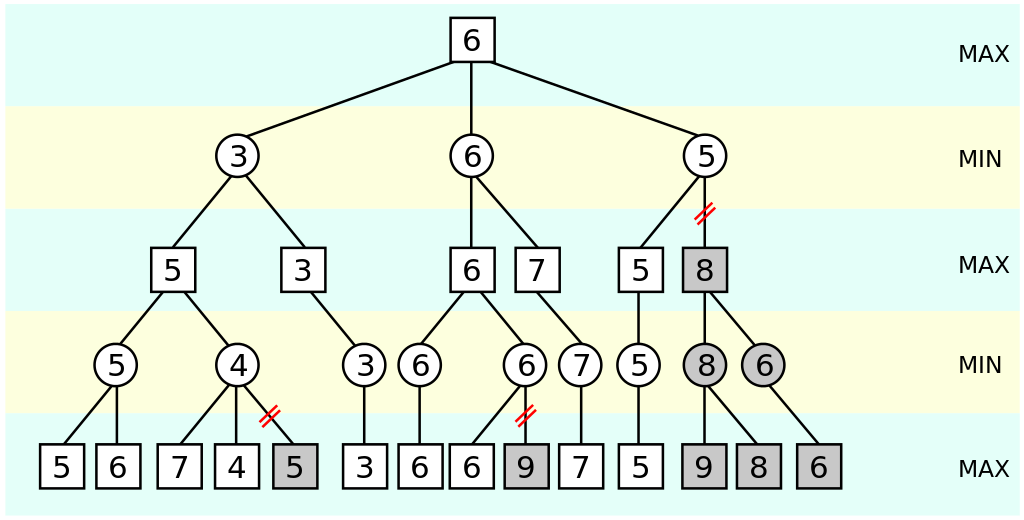
alpha-beta pruning in progress - low value branches are abandoned
Alpha-beta pruning. Lower scores are better. Branches that cannot achieve the low scores of other branches are abandoned. Original image
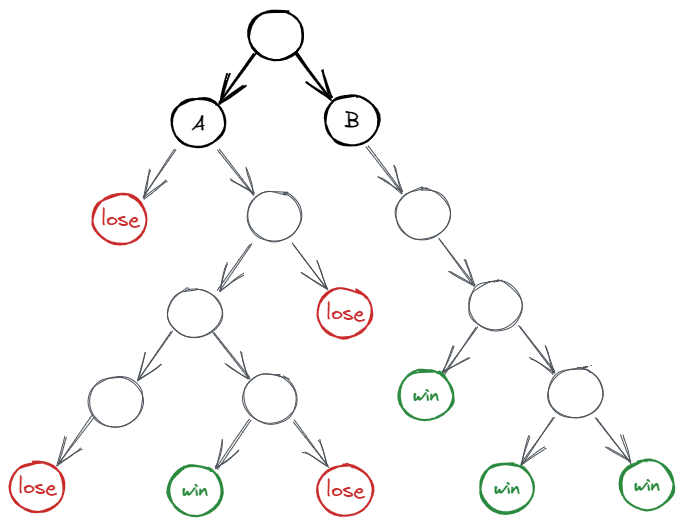
outcomes of multiple game playthroughs, represented as a graph of game states
A representation of MCTS 'rollout'. After playing a number of games from the current state, branch B looks the most promising.

The above images show that MCTS is more akin to depth-first search, while alpha-beta pruning is breadth-first.

To create a generic MCTS bot with OpenSpiel:

bot = mcts.MCTSBot(
    game,
    uct_c=math.sqrt(2),
    max_simulations=2,
    evaluator=mcts.RandomRolloutEvaluator(n_rollouts=1))

Off to a good start

I wrapped Andoma in an OpenSpiel bot interface (see below). It took a bit of learning about chess notation to map pychess’s moves to the valid moves presented by OpenSpiel’s chess implementation. See the appendix for the notation used in this post. You can see the full code from my bot_vs_bot.py script.

class AndomaBot(pyspiel.Bot):
  def __init__(self, search_depth=1):
    pyspiel.Bot.__init__(self)
    self.search_depth = search_depth

  def step(self, state: pyspiel.State) -> int:
    board = chess.Board(str(state))
    move = movegeneration.next_move(self.search_depth, board, debug=False)
    return self._pychess_to_spiel_move(move, state)

  def _pychess_to_spiel_move(self, move: chess.Move, state: pyspiel.State):
    # This is necessary, as openspiel's chess move notation sometimes differs
    # from pychess's. Details omitted for brevity.

With that thin wrapper, I had the MCTS and Andoma bots fighting! My MCTS bot was winning every game, even when Andoma’s search depth was set to 3 (slow!), and MCTS only doing 2 full game simulations per move. After the few seconds of elation at being an instant master game AI programmer, I figured I’d made a mistake somewhere.

Oops

Here was my problem:

player_label = ['mcts', 'andoma']
winner = player_label[0] if winner_idx == 0 else player_label[0]

Derp. Happens to the best of us.

With that fixed, I found that Andoma was winning every game, even when its search depth was set to 1, and MCTS was doing 10 full game simulations, each with 10 rollouts per search node. Each game was taking about a minute to run at these settings, so I gave up there. This result makes more sense. Even though MCTS is simulating many games, the simulated moves are random, which is hardly an effective strategy for playing chess. Andoma encodes a lot of knowledge about chess, thus is able to make moves that are much better than random moves!

Even when playing against a random bot, MCTS didn’t win all its games. It had a decent win rate once the number of simulations and rollouts were > 6, but these games were taking close to a minute to run. I won’t be entering my chess bot in any speed chess competitions soon. For comparison, Andoma wins every game against a random opponent, even at a search depth of 1, which takes at most a few seconds to run.

An experiment: MCTS with Andoma rollout

Rather than simulating games by making random moves, what about using Andoma’s move evaluation to greedily pick the ‘best’ move at each game state? This was easy to try, as the OpenSpiel MCTS implementation allows for easy swapping of ’evaluator’ implementations (one being the neural network used by AlphaGo). I plugged in this evaluator:

class AndomaValuesRolloutEvaluator:
  def evaluate(self, state):
    """ 'Rolls out' a complete game, returning the outcome.
        There's no need for multiple rollouts, since Andoma's
        move choice is deterministic.
    """
    working_state = state.clone()
    while not working_state.is_terminal():
      action = self._best_action(working_state)
      working_state.apply_action(action)
    return np.array(working_state.returns())

  def _best_action(self, state: pyspiel.State) -> int:
    board = chess.Board(str(state))
    # return the 'best' move decided by Andoma's move ordering
    move = get_ordered_moves(board)[0]
    return self._pychess_to_spiel_move(move, state)

Coupled with this evaluator, MCTS was able to beat a random bot more often. However, its performance (execution time) was pretty hopeless. A quick look at the profiler results (python -m cProfile -s time my_slow_program.py FTW!) showed that the translation of moves between OpenSpiel and pychess was taking up a lot of time. I decided that this was a good place to stop - my main interest was in creating a bot that could play chess with zero knowledge (outside of the game rules), and this experiment was just for curiosity’s sake.

What next?

I’ve just finished part one of Reinforcement Learning: An Introduction, which is all about ’tabular’ methods. These are algorithms that learn by storing all observed states and estimating each state’s value through many playthroughs of the game. These methods are impractical for chess, which apparently has more possible game states than there are atoms in the universe!

Part two of the book covers approximation strategies, which are essentially mandatory for anything but trivially small AI problems like tic-tac-toe. My plan is to read this, then come back with a vengeance.

Appendix: chess notation

I had to learn a bunch of chess notation to be able to build these bots. Here’s what I learned.

Chess pieces

The notation systems here use the following characters to denote chess pieces:

Lowercase letters are black pieces, uppercase are white.

Forsyth-Edwards Notation (FEN)

FEN describes the current state of a chess game with a line of characters. There’s plenty of descriptions of FEN on the internet. If you want more details, here’s one. Here’s my crash course.

A FEN string looks like this:

rnbqk1nr/p1ppppbp/1p4p1/8/2P5/2Q5/PP1PPPPP/RNB1KBNR b KQkq - 0 1

The first chunk of characters describes the position of the chess pieces. The above string translates to:

r n b q k . n r
p . p p p p b p
. p . . . . p .
. . . . . . . .
. . P . . . . .
. . Q . . . . .
P P . P P P P P
R N B . K B N R

The characters after the piece positions:

rnbqk1nr/p1ppppbp/1p4p1/8/2P5/2Q5/PP1PPPPP/RNB1KBNR b KQkq - 0 1
───────────┬───────────   ────────────┬──────────── ▲ ──┬─ ▲ ▲ ▲
           │                          │             │   │  │ │ └─fullmove counter
           │                          │             │   │  │ │
           │                          │             │   │  │ └───halfmove clock
           │                          │             │   │  │
           │                          │             │   │  └─────en passant targets
           │                          │             │   │
           │                          │             │   └────────castling rights, white, black
           │                          │             │
           │                          │             └────────────black's move
           │                          │
           │                          └──────────────────────────white pieces are uppercase
           │
           └─────────────────────────────────────────────────────black pieces are lowercase

Move notation

FEN only describes the current game state, not moves that occur within the game. There are multiple notations, but algebraic notation seems to be pretty common.

Rank & file

rank
   |
   v

   8   r n b q k . n r
   7   p . p p p p b p
   6   . p . . . . p .
   5   . . . . . . . .
   4   . . P . . . . .
   3   . . Q . . . . .
   2   P P . P P P P P
   1   R N B . K B N R

       a b c d e f g h   <-- file

Moves

Moves are denoted by the letter specifying the piece, and the board position it moves to. Pawn moves don’t use a letter specifier. For example:

Note that without knowledge of the current game state, there is ambiguity in this move notation: for example, ‘a3’ could mean different moves, depending on the current game state.

References